Motivation

Point Cloud:

  1. disordered (permutation-invariant )
  2. unstructured

which make it difficult to designing a neural networks to process.

All operations of Transformer are parallelizable and order-independent , which is suitable for PT feature learning.

In NLP ,the classical Transformer use the positional encoding to deal with the order-independence .

the input of word is in order, and word has basic semantic, whereas point clouds are unordered, and individual points have no semantic meaning in general.

Therefore，we need to modify the classical Transformer structure！

overall

1

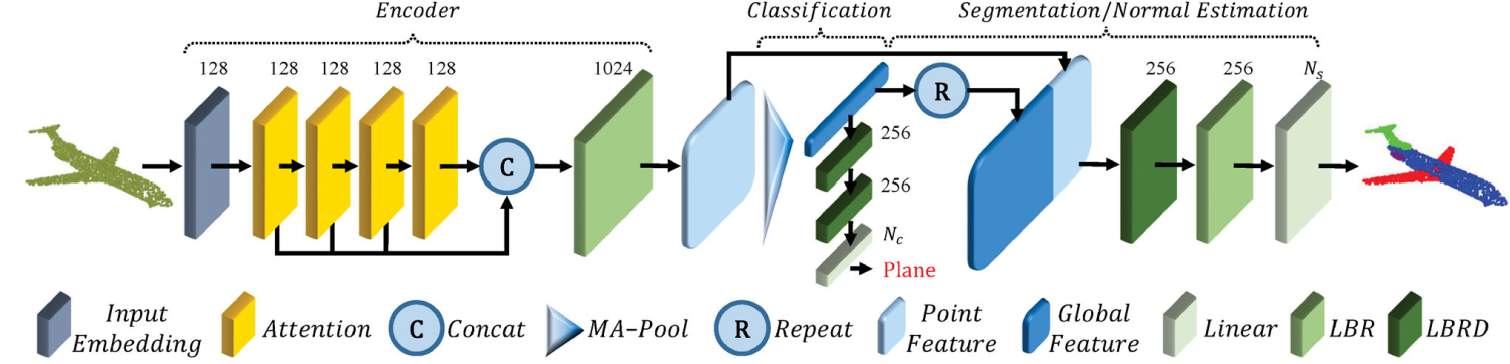
Offset-Attention and Naive Self-Attention

2

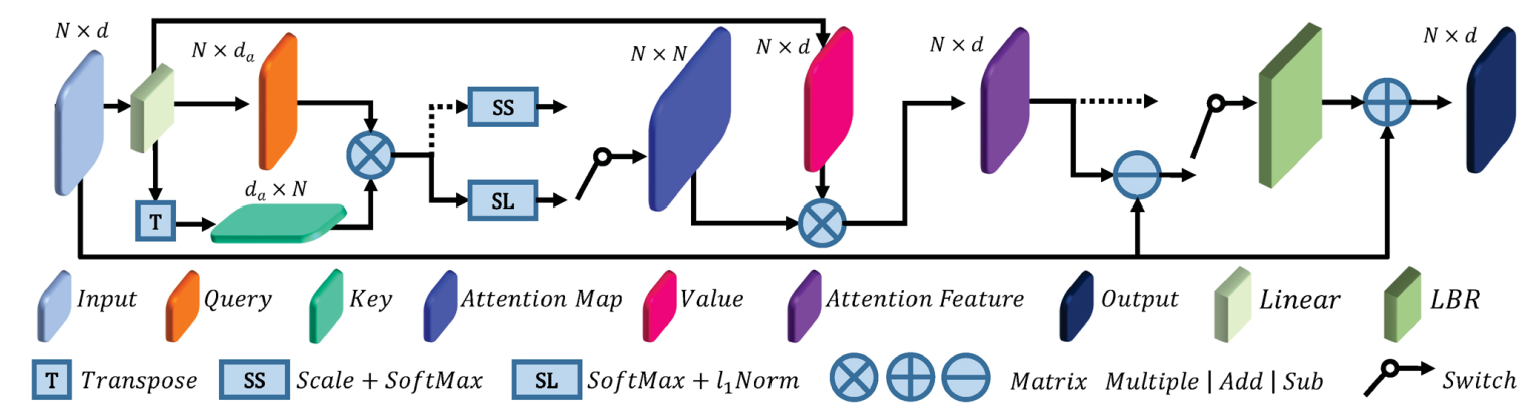
The dotted line represents the Self-Attention

Offset-Attention

Inspired by the Laplacian Matrix in GCN, the paper proposes the Offset-Attention structure.

  • original:

Fout=SA(Fin)=LBR(Fsa)+Fin\boldsymbol{F}_{out}=\mathrm{SA}(\boldsymbol{F}_{in})=\mathrm{LBR}(\boldsymbol{F}_{sa})+\boldsymbol{F}_{in}

  • modified:

Fout=OA(Fin)=LBR(Fin−Fsa)+Fin\boldsymbol{F}_{out}=\mathrm{OA}(\boldsymbol{F}_{in})=\mathrm{LBR}(\boldsymbol{F}_{in}-\boldsymbol{F}_{sa})+\boldsymbol{F}_{in}

Fin−Fsa=Fin−AV=Fin−AFinWv≈Fin−AFin=(I−A)Fin≈LFin\begin{aligned} \boldsymbol{F}_{in}-\boldsymbol{F}_{sa}& =F_{in}-AV \\ &=F_{in}-AF_{in}W_v \\ &\approx F_{in}-AF_{in} \\ &=(I-A)F_{in}\approx LF_{in} \end{aligned}

Here,Fin−FsaF_{in}-F_{sa} is analogous to a discrete Laplacian operator.

II is an identity matrix comparable to the diagonal degree matrix DD of the Laplacian matrix and AA is the attention matrix comparable to the adjacency matrix EE

  • Inspired : Graph convolution networks show the benefits of using a Laplacian matrix L=D−EL = D - E to replace the adjacency matrix EE. That is, Laplacian operator is more capable of extracting global feature

softmax and l1_norm

  • original: scaled and softmax

    αˉi,j=α~i,jdaαi,j=softmax(αˉi,j)=exp⁡(αˉi,j)∑kexp⁡(αˉi,k)\begin{aligned}&\bar{\alpha}_{i,j}=\frac{\tilde{\alpha}_{i,j}}{\sqrt{d_{a}}}\\&\alpha_{i,j}=\mathrm{softmax}(\bar{\alpha}_{i,j})=\frac{\exp{(\bar{\alpha}_{i,j})}}{\sum_{k}\exp{(\bar{\alpha}_{i,k})}}\end{aligned}

  • modified: softmax followed by l1_norm

  • αˉi,j=softmax(α~i,j)=exp⁡(α~i,j)∑kexp⁡(α~k,j)αi,j=αˉi,j∑kαˉi,k\begin{aligned}&\bar{\alpha}_{i,j}=\mathrm{softmax}(\tilde{\alpha}_{i,j})=\frac{\exp{(\tilde{\alpha}_{i,j})}}{\sum_{k}\exp{(\tilde{\alpha}_{k,j})}}\\&\alpha_{i,j}=\frac{\bar{\alpha}_{i,j}}{\sum_{k}\bar{\alpha}_{i,k}}\end{aligned}

Our offset-attention sharpens the attention weights and reduces the influence of noise, which is beneficial for downstream tasks.

Neighbor embedding

PCT with point embedding is an effective network for extracting global features.

3
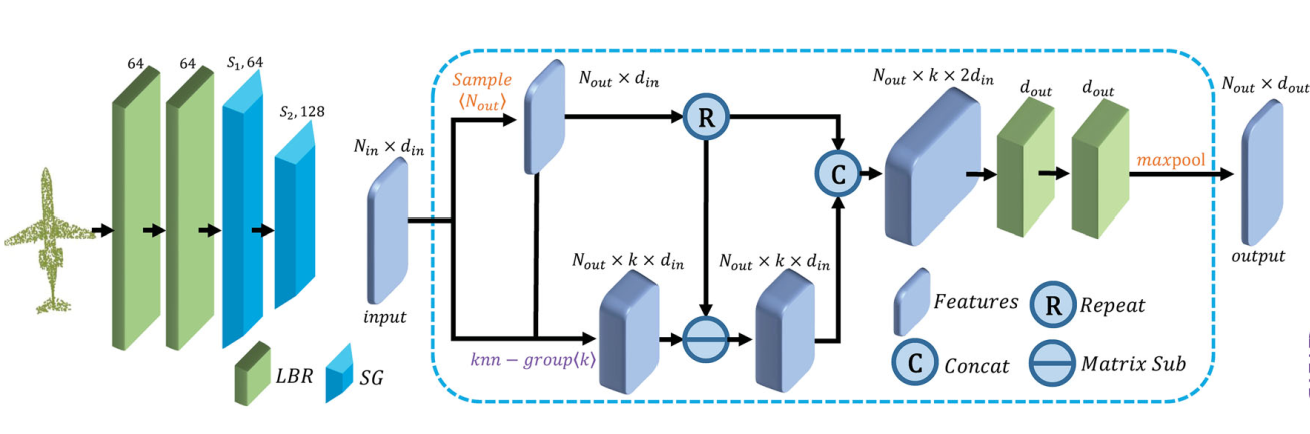
  1. use farthest point sampling (FPS) algorithm to down sample to (find the cluster center)
  2. use k nearest neighbor (knn) algorithm to find their neighborhood
  3. The neighbor information is aggerated.