motivation:diffusion model for planning
diffusion model 现在很多应用在traffic simulation 上,在用 diffusion model 做 plan的没有。
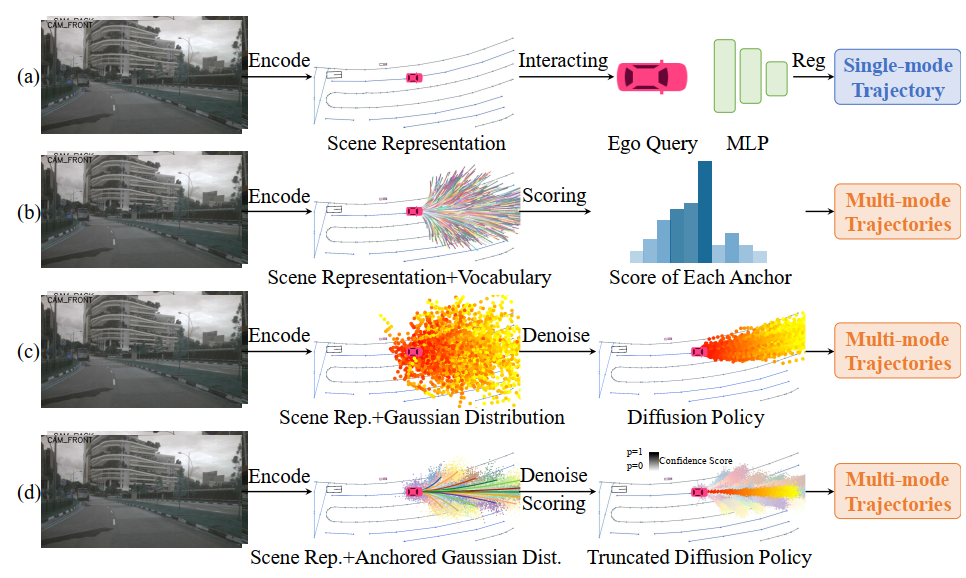
(a): this paradigm does not account for the inherent uncertainty and multi-mode nature of driving behaviors.
无法表示 uncertainty
(b): this large fixed-vocabulary paradigm is fundamentally constrained by the number and quality of anchor trajectories, often failing in out-of-vocabulary scenarios. Furthermore, managing a large number of anchors presents significant computational challenges for real-time applications.[VAD-v2]
依赖于锚点的数量和质量,action空间离散
©: 推断延迟太高
contribution
- diffusion model to end to end autonomous drive plan
- design an efficient transformer-based diffusion decoder that interacts with the conditional information in a cascaded manner for better trajectory reconstruction 改进了传统diffusion --> Truncated Diffusion
- sota and diversity
overall
TransfuserDP(vanilla scheme)
We begin from the representative deterministic end-to-end planner Transfuser and turn it into a generative model TransfuserDP by simply replacing the regression MLP layers with the conditional diffusion model UNet following vanilla diffusion policy .
存在的问题
- Mode collapse : diversity 很低
- Heavy denoising overhead : inference 速度很慢
Truncated Diffusion
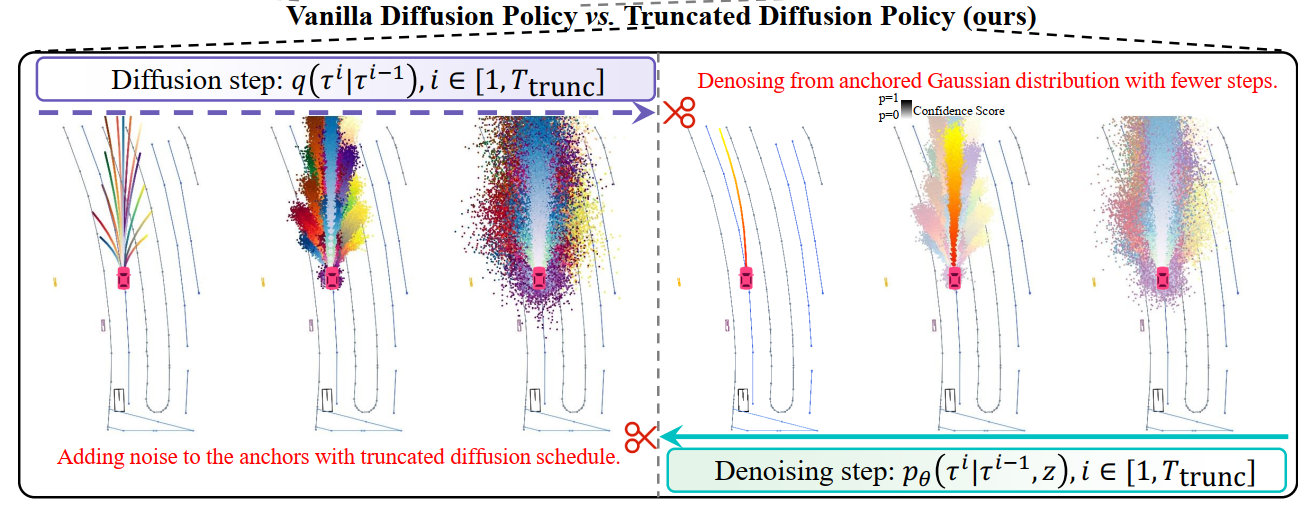
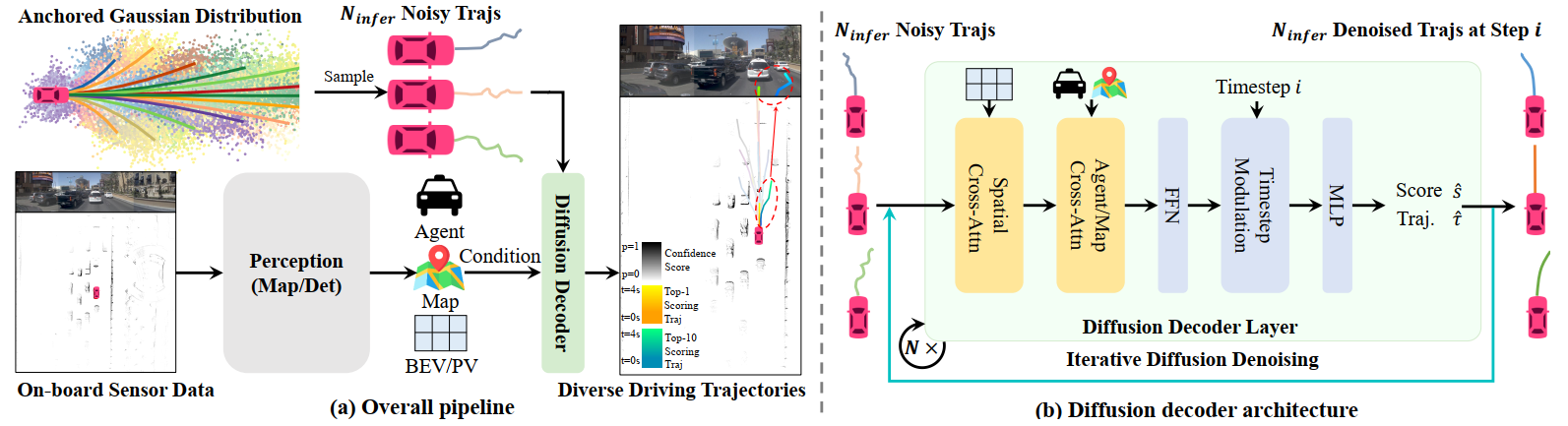
前向过程: We first construct the diffusion process by adding Gaussian noise to anchors clustered by K-Means on the training set, where . We truncate the diffusion noise schedule to diffuse the anchors to the anchored Gaussian distribution:
where and is the truncated diffusion steps.
sample 出 个noisy轨迹。
反向过程(diffusion decoder):the diffusion decoder takes as input noisy trajectories and predicts classification scores and denoised trajectories .
where represents the conditional information.
把这个noisy轨迹恢复为个轨迹路线。
损失函数 We assign the noisy trajectory around the closest anchor to the ground truth trajectory as positive sample and others as negative samples . The training objective combines trajectory reconstruction and classification:
where balances the simple L1 reconstruction loss and binary cross-entropy (BCE) classification loss.
Inference. We use a truncated denoising process that starts with noisy trajectories sampled from the anchored Gaussian distribution and progressively denoises them to final predictions. At each denoising timestep, the estimated trajectories from the previous step are passed to the diffusion decoder , which predicts classification scores and coordinates . After obtaining the current timestep’s predictions, we apply the DDIM update rule to sample trajectories for the next timestep.
Inference flexibility. A key advantage of our approach lies in its inference flexibility. While the model is trained with trajectories, the inference process can accommodate an arbitrary number of trajectory samples , where can be dynamically adjusted based on computational resources or application requirements.
实验
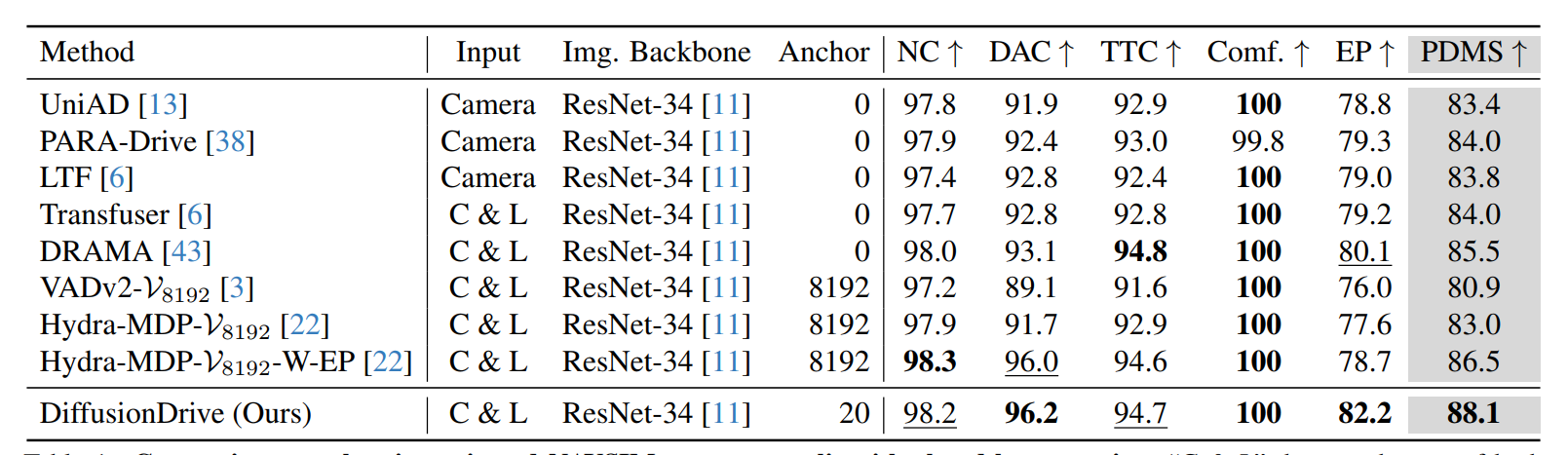
数据集:NAVSIM navtest split