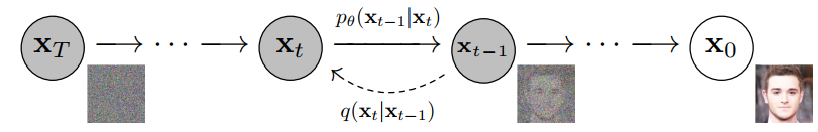生成模型对比

img

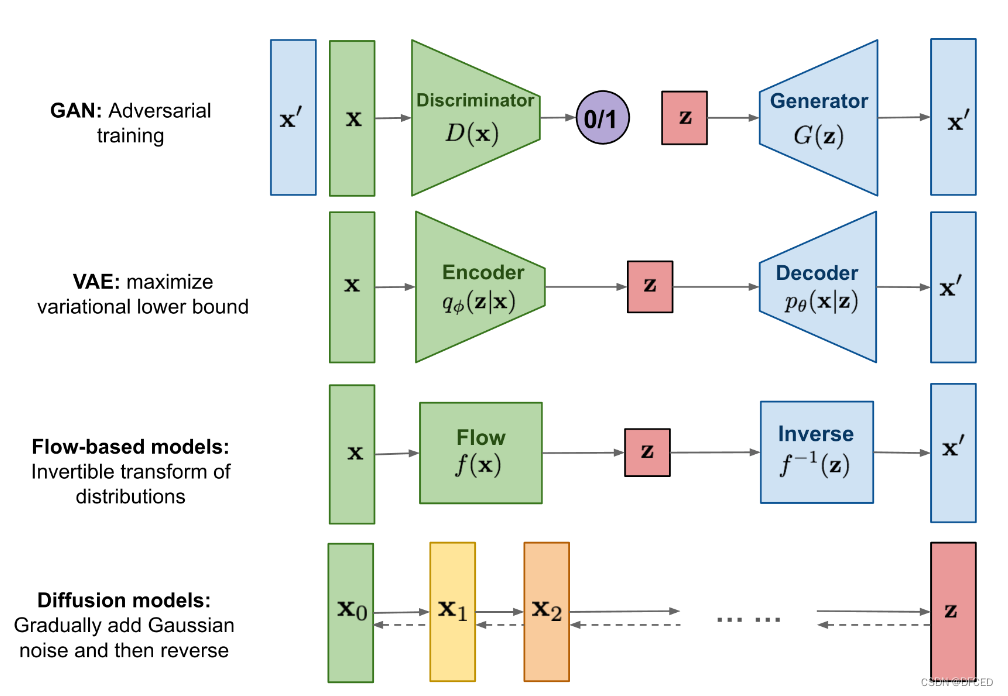
GAN网络由discriminator和generator组成，discriminator致力于区分x和x‘，而generator致力于生成尽可能通过discriminator的样本，迭代多次，最终generator生成的样本越来越像x，即我们需要的生成式样本。

VAE是学习分布函数的网络，但是这里的分布函数是从样本空间到语义空间的。

Flow-based models是真正开始学习分布的网络结构

overall

1

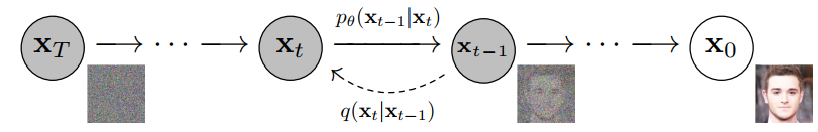
forward process (diffusion process 扩散过程)：从右到左 X0→XTX_0 \rightarrow X_T

reverse process (denoising process 去噪过程)：从左到右 XT→X0X_{T}\rightarrow X_0

扩散过程和去噪过程，都视为Markov 过程。

x0∼q(x0)x_0 \sim q(x_0)

任务为：学习一个分布(distribution ) pθ(x0:T)p_{\theta}(\mathbf{x}_{0:T}),并使用pθ(x0):=∫pθ(x0:T)dx1:Tp_\theta(\mathbf{x}_0):=\int p_\theta(\mathbf{x}_{0:T}) d\mathbf{x}_{1:T}来估计q(x0)q(x_0)。

具体来说，在训练过程中，这是一个扩散过程，markov转移方程q(xt∣xt−1)q(x_t|x_{t-1})为高斯分布，并且它的参数是不需要学习的，也就是说q(x0:T)q(\mathbf{x}_{0:T})是已知的；在生成过程中，markov的转移方程q(xt−1∣xt)q(x_{t-1}|x_t)也是高斯分布，但是q(xt−1∣xt)q(x_{t-1}|x_t)是无法计算的，只能通过学习即pθ(xt−1∣xt)p_{\theta}(x_{t-1}|x_t)来近似估计。

这里注意两点

  1. pθ(xt−1∣xt)p_{\theta}(x_{t-1}|x_t) 应该为高斯分布，但是它的参数是学习出来的
  2. 在扩散过程中学习出这些参数

loss function: (不方便使用交叉熵 i.e. 最大似然估计)

Eq[−log⁡pθ(x0)]≤Eq[−log⁡pθ(x0:T)q(x1:T∣x0)]=Eq[−log⁡p(xT)−∑t≥1log⁡pθ(xt−1∣xt)q(xt∣xt−1)]=:L\mathbb{E}_q\left[-\log p_\theta(\mathbf{x}_0)\right]\leq\mathbb{E}_q\bigg[-\log\frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T}|\mathbf{x}_0)}\bigg]=\mathbb{E}_q\bigg[-\log p(\mathbf{x}_T)-\sum_{t\geq1}\log\frac{p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)}{q(\mathbf{x}_t|\mathbf{x}_{t-1})}\bigg]=:L

扩散过程

扩散过程是一个转移函数为高斯函数的markov 过程：

q(x1:T∣x0):=∏t=1Tq(xt∣xt−1),q(xt∣xt−1):=N(xt;1−βtxt−1,βtI)q(\mathbf{x}_{1:T}|\mathbf{x}_0):=\prod_{t=1}^Tq(\mathbf{x}_t|\mathbf{x}_{t-1}),\quad q(\mathbf{x}_t|\mathbf{x}_{t-1}):=\mathcal{N}(\mathbf{x}_t;\sqrt{1-\beta_t}\mathbf{x}_{t-1},\beta_t\mathbf{I})

这里βt\beta_t在文章中设置为超参数，βt∈(0,1)\beta_t \in(0,1)，并且随着t单调递增，文章中取βt\beta_t为0.001到0.02。

在任何时刻t，使用求边缘概率分布或者参数重组方式，可以得到：

q(xt∣x0)=N(xt;αˉtx0,(1−αˉt)I)αt:=1−βt and αˉt:=∏s=1tαsq(\mathbf{x}_t|\mathbf{x}_0)=\mathcal{N}(\mathbf{x}_t;\sqrt{\bar{\alpha}_t}\mathbf{x}_0,(1-\bar{\alpha}_t)\mathbf{I})\\\\ \alpha_{t}:=1-\beta_{t}\mathrm{~and~}\bar{\alpha}_{t}:=\prod_{s=1}^{t}{\alpha}_{s}

也可以认为：xtx_t为x0x_0的仿射变换

xt=αˉtx0+(1−αˉt)ϵϵ∼Nd(0,1)\mathbf {x_t}=\sqrt{\bar{\alpha}_t}\mathbf{x}_0+\sqrt{(1-\bar{\alpha}_t)}\epsilon\\\\ \epsilon\sim\mathcal{N_d}(0,1)

此时将loss 函数继续改写：

L:=Eq[DKL(q(xT∣x0)∥p(xT))⏟LT+∑t>1DKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))⏟Lt−1−log⁡pθ(x0∣x1)⏟L0]\mathbf{L}:=\mathbb{E}_q\bigg[\underbrace{D_{\mathrm{KL}}(q(\mathbf{x}_T|\mathbf{x}_0)\parallel p(\mathbf{x}_T))}_{L_T}+\sum_{t>1}\underbrace{D_{\mathrm{KL}}(q(\mathbf{x}_{t-1}|\mathbf{x}_t,\mathbf{x}_0)\parallel p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t))}_{L_{t-1}}\underbrace{-\log p_\theta(\mathbf{x}_0|\mathbf{x}_1)}_{L_0}\bigg]

我们使用贝叶斯公式来求 q(xt−1∣xt,x0)q(\mathbf{x}_{t-1}|\mathbf{x}_t,\mathbf{x}_0):

q(xt−1∣xt,x0)=q(xt∣xt−1,x0)q(xt−1∣x0)q(xt∣x0)∝exp⁡(−12((xt−αtxt−1)2βt+(xt−1−α‾t−1x0)21−a‾t−1−(xt−α‾tx0)21−a‾t))q(xt−1∣xt,x0)=N(xt−1;μ~t(xt,x0),βtI),whereμ~t(xt,x0):=αˉt−1βt1−αˉtx0+αt(1−αˉt−1)1−αˉtxtandβ~t:=1−αˉt−11−αˉtβt\begin{aligned} q(x_{t-1}|x_t,x_0)& =q(x_t|x_{t-1},x_0)\frac{q(x_{t-1}|x_0)}{q(x_t|x_0)} \\ &\propto\exp\left(-\frac{1}{2}\Big(\frac{(x_{t}-\sqrt{\alpha_{t}}x_{t-1})^{2}}{\beta_{t}}+\frac{(x_{t-1}-\sqrt{\overline{\alpha}_{t-1}}x_{0})^{2}}{1-\overline{a}_{t-1}}-\frac{(x_{t}-\sqrt{\overline{\alpha}_{t}}x_{0})^{2}}{1-\overline{a}_{t}}\Big)\right)\\ q(\mathbf{x}_{t-1}|\mathbf{x}_{t},\mathbf{x}_{0})& =\mathcal{N}(\mathbf{x}_{t-1};\tilde{\boldsymbol{\mu}}_{t}(\mathbf{x}_{t},\mathbf{x}_{0}),\beta_{t}\mathbf{I}), \\ \mathrm{where}\quad\tilde{\mu}_t(\mathbf{x}_t,\mathbf{x}_0)& :=\frac{\sqrt{\bar{\alpha}_{t-1}}\beta_{t}}{1-\bar{\alpha}_{t}}\mathbf{x}_{0}+\frac{\sqrt{\alpha_{t}}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_{t}}\mathbf{x}_{t}\quad\mathrm{and}\quad\tilde{\beta}_{t}:=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_{t}}\beta_{t} \end{aligned}

继续做变换（参数重组）：

x0=1αˉt(xt−(1−αˉt)ϵ)ϵ∼Nd(0,1)\mathbf {x_0}=\frac{1}{\sqrt{\bar{\alpha}_t}}(\mathbf{x}_t-\sqrt{(1-\bar{\alpha}_t)}\epsilon)\\\\ \epsilon\sim\mathcal{N_d}(0,1)

得到

μ~t(xt,x0)=1αt(xt−βt1−αˉtϵ)β~t:=1−αˉt−11−αˉtβt\tilde{\mu}_t(\mathbf{x}_t,\mathbf{x}_0)=\frac1{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\boldsymbol{\epsilon}\right)\\ \quad\tilde{\beta}_{t}:=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_{t}}\beta_{t}

降噪过程

我们需要根据扩散过程和loss函数来确定pθp_{\theta}：

  1. 在训练时 LTL_{T}是一个常数，因为qq的各参数已知，而xt\mathbf{x}_t在降噪过程中也是给出的
  2. L0L_0也可以不用考虑，因为β1\beta_1很小，也就是说，在扩散过程中，x1x_1相对于x0x_0加的噪声很小，文章中实际上没必要生成x0x_0，后续文章中写到最终生成的其实是μθ(x1,1)\boldsymbol{\mu}_\theta(\mathbf{x}_1,1)。
  3. Lt−1L_{t-1}才是真正需要考虑的

根据loss函数中Lt−1L_{t-1}来看，我们需要使用 pθ(xt−1∣xt)p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t) 来逼近 q(xt−1∣xt,x0)q(\mathbf{x}_{t-1}|\mathbf{x}_t,\mathbf{x}_0) ，那么显然 pθ(xt−1∣xt)p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t) 也必须为高斯分布：

pθ(xt−1∣xt)=N(xt−1;μ~θ(xt,t),σt2I)p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})=\mathcal{N}(\mathbf{x}_{t-1};\tilde{\boldsymbol{\mu}}_{\theta}(\mathbf{x}_{t},t),\sigma_{t}^{2}\mathbf{I})

这里需要注意的是，q(xt−1∣xt,x0)q(\mathbf{x}_{t-1}|\mathbf{x}_{t},\mathbf{x}_{0})化简后实际上只和βt,xt,ϵ\beta _t,x_t,\epsilon有关，βt\beta _t已知，xtx_t是给出的，所以最关键的就是如何估计ϵ\epsilon。

ϵ\epsilon其实是从x0\mathbf{x_0}到xt\mathbf{x_t}所加的噪声（标准化过），在降噪过程中，我们应该将ϵ\epsilon视为一种待估计的量，实际上就是数理统计中参数估计。传统数理统计中有很多办法，文章中使用神经网络做估计，在数理统计的观点下，机器学习的目标就是学习一个好的样本统计量 。

形式化后就是：

μ~θ(xt,t)=1αt(xt−βt1−αˉtϵθ(xt,t))σt2=β~t=1−αˉt−11−αˉtβt\tilde{\boldsymbol{\mu}}_\theta(\mathbf{x}_t,t)=\frac1{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\boldsymbol{\epsilon}_\theta(\mathbf{x}_t,t)\right)\\ \sigma_{t}^{2} = \tilde{\beta}_{t} = \frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_{t}}\beta_{t}

参数重组后，得到xt−1x_{t-1}和xtx_t的关系为：

xt−1=μ~θ(xt,t)+σtz;z∼Nd(0,1)xt−1=1αt(xt−1−αt1−αˉtϵθ(xt,t))+σtz\mathbf{x}_{t-1}=\tilde{\boldsymbol{\mu}}_\theta(\mathbf{x}_t,t)+\sigma_{t}\mathbf{z};\mathbf{z}\sim\mathcal{N_d}(0,1)\\ \mathbf{x}_{t-1}=\frac{1}{\sqrt{\alpha_{t}}}\left(\mathbf{x}_{t}-\frac{1-\alpha_{t}}{\sqrt{1-\bar{\alpha}_{t}}}\boldsymbol{\epsilon}_{\theta}(\mathbf{x}_{t},t)\right)+\sigma_{t}\mathbf{z}

算法

重新改写一下loss 函数最终变为

L(θ)=Ex0,ϵ[βt22σt2αt(1−αˉt)∥ϵ−ϵθ(αˉtx0+1−αˉtϵ,t)∥2]Lsimple(θ):=Et,x0,ϵ[∥ϵ−ϵθ(αˉtx0+1−αˉtϵ,t)∥2]L(\theta)=\mathbb{E}_{\mathbf{x}_0,\boldsymbol{\epsilon}}\left[\frac{\beta_t^2}{2\sigma_t^2\alpha_t(1-\bar{\alpha}_t)}\left\|\boldsymbol{\epsilon}-\boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0+\sqrt{1-\bar{\alpha}_t}\boldsymbol{\epsilon},t)\right\|^2\right] \\ L_{\mathrm{simple}}(\theta):=\mathbb{E}_{t,\mathbf{x}_0,\boldsymbol{\epsilon}}\Big[\left\|\boldsymbol{\epsilon}-\boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0+\sqrt{1-\bar{\alpha}_t}\boldsymbol{\epsilon},t)\right\|^2\Big]

image-20241111074243631

这里的ϵθ()\epsilon_\theta()模型可以选很多种，文章中采用的是UNET。