Problem scenario
已知隐变量的先验分布和条件生成分布
以上背景下的相关问题有:
Preliminary
evidence lower bound (variational lower bound)
推断(inference)可以理解为计算后验分布P ( Z ∣ X ) P(Z|X) P ( Z ∣ X )
P ( Z ∣ X ) = P ( X , Z ) ∫ z P ( X , Z = z ) d z P(Z|X)=\frac{P(X,Z)}{\int_z{P(X,Z=z)}dz}
P ( Z ∣ X ) = ∫ z P ( X , Z = z ) d z P ( X , Z )
其中分母(规范项)很难计算,所以精确计算后验分布很困难,常常有两种方法求解近似的后验分布。
采样法:例如MCMC,MCMC方法是利用马尔科夫链取样来近似后验概率,它的计算开销很大,且精度和样本有关系。
变分法:使用一个简单的概率分布来近似后验分布,于是就转换为一个优化问题
KL divergence:
D K L ( q ∣ ∣ p ) = E x ∼ q [ log p q ] = ∑ x q ( x ) log p ( x ) q ( x ) D_{KL}(q||p)=E_{x\sim q}[\log{\frac{p}{q}}]=\sum_{x}q(x)\log\frac{p(x)}{q(x)}
D K L ( q ∣∣ p ) = E x ∼ q [ log q p ] = x ∑ q ( x ) log q ( x ) p ( x )
KL divergence是衡量两个分布的距离的,它具有非负性,越小两个分布越接近。
变分法使用简单的概率分布q ( z ) q(z) q ( z ) p ( z ∣ x ) p(z|x) p ( z ∣ x ) q ( z ) q(z) q ( z )
λ ∗ = arg min λ D K L ( q ( z ) ∣ ∣ p ( z ∣ x ) ) (1) \lambda^*=\arg \min_{\lambda}D_{KL}(q(z)||p(z|x)) \tag{1}
λ ∗ = arg λ min D K L ( q ( z ) ∣∣ p ( z ∣ x )) ( 1 )
注意:这里λ \lambda λ λ \lambda λ
log p ( x ) = log p ( x , z ) q ( z ) − log p ( z ∣ x ) q ( z ) E q ( z ) [ log p ( x ) ] = E q ( z ) [ log p ( x , z ) q ( z ) ] − E q ( z ) [ log p ( z ∣ x ) q ( z ) ] log p ( x ) = D K L ( q ( z ) ∣ ∣ p ( z ∣ x ) ) + E q ( z ) [ log p ( x , z ) q ( z ) ] \log p(x)=\log\frac{p(x,z)}{q(z)}-\log\frac{p(z|x)}{q(z)}\\
E_{q(z)}[\log p(x)]=E_{q(z)}[\log\frac{p(x,z)}{q(z)}]-E_{q(z)}[\log\frac{p(z|x)}{q(z)}]\\
\log p(x)=D_{KL}({q(z)||p(z|x)})+E_{q(z)}[\log\frac{p(x,z)}{q(z)}]
log p ( x ) = log q ( z ) p ( x , z ) − log q ( z ) p ( z ∣ x ) E q ( z ) [ log p ( x )] = E q ( z ) [ log q ( z ) p ( x , z ) ] − E q ( z ) [ log q ( z ) p ( z ∣ x ) ] log p ( x ) = D K L ( q ( z ) ∣∣ p ( z ∣ x ) ) + E q ( z ) [ log q ( z ) p ( x , z ) ]
其中log p ( x ) \log p(x) log p ( x ) E q ( z ) [ log p ( x , z ) q ( z ) ] E_{q(z)}[\log\frac{p(x,z)}{q(z)}] E q ( z ) [ log q ( z ) p ( x , z ) ]
则(1)式转化为:
λ ∗ = arg max λ E L B O = arg max λ E q ( z ) [ log p ( x , z ) q ( z ) ] (2) \lambda^*=\arg \max_{\lambda}ELBO=\arg \max_{\lambda}E_{q(z)}[\log\frac{p(x,z)}{q(z)}]\tag{2}
λ ∗ = arg λ max E L BO = arg λ max E q ( z ) [ log q ( z ) p ( x , z ) ] ( 2 )
有了(2)式就可以利用一些优化技巧来求解得到λ ∗ \lambda^* λ ∗
黑盒变分推断
例如黑盒变分推断,对ELBO进行求导:
∇ λ E L B O = ∇ λ E z ∼ q ( z ) [ log p ( x , z ) − log q ( z ) ] = ∇ λ ∫ q ( z ) [ log p ( x , z ) − log q ( z ) ] d z = ∫ log p ( x , z ) ∇ λ q ( z ) − q ( z ) ∇ λ log q ( z ) − log q ( z ) ∇ λ q ( z ) d z ∇ λ log q ( z ) = ∇ λ q ( z ) q ( z ) 带入上式 = ∫ q ( z ) log p ( x , z ) ∇ λ log q ( z ) − ∇ λ q ( z ) − q ( z ) log q ( z ) ∇ λ log q ( z ) d z = ∫ q ( z ) log p ( x , z ) ∇ λ log q ( z ) − q ( z ) log q ( z ) ∇ λ log q ( z ) d z = E z ∼ q ( z ) [ ( log p ( x , z ) − log q ( z ) ) ∇ λ log q ( z ) ] \begin{aligned}
\nabla_{\lambda}ELBO=&\nabla_{\lambda}E_{z\sim q(z)}[\log p(x,z)-\log q(z)]\\
=&\nabla_{\lambda}\int q(z) [\log p(x,z)-\log q(z)]dz\\
=&\int \log p(x,z)\nabla_{\lambda} q(z) -q(z)\nabla_{\lambda}\log q(z)-\log q(z)\nabla_{\lambda}q(z)dz\\
&\nabla_{\lambda}\log q(z)=\frac{\nabla_{\lambda}q(z)}{q(z)}\text{带入上式}\\
=&\int q(z)\log p(x,z)\nabla_{\lambda} \log q(z) -\nabla_{\lambda}q(z)-q(z)\log q(z)\nabla_{\lambda}\log q(z)dz\\
=&\int q(z)\log p(x,z)\nabla_{\lambda} \log q(z) -q(z)\log q(z)\nabla_{\lambda}\log q(z)dz\\
=&E_{z\sim q(z)}[ (\log p(x,z)-\log q(z))\nabla_{\lambda} \log q(z) ]\\
\end{aligned}
∇ λ E L BO = = = = = = ∇ λ E z ∼ q ( z ) [ log p ( x , z ) − log q ( z )] ∇ λ ∫ q ( z ) [ log p ( x , z ) − log q ( z )] d z ∫ log p ( x , z ) ∇ λ q ( z ) − q ( z ) ∇ λ log q ( z ) − log q ( z ) ∇ λ q ( z ) d z ∇ λ log q ( z ) = q ( z ) ∇ λ q ( z ) 带入上式 ∫ q ( z ) log p ( x , z ) ∇ λ log q ( z ) − ∇ λ q ( z ) − q ( z ) log q ( z ) ∇ λ log q ( z ) d z ∫ q ( z ) log p ( x , z ) ∇ λ log q ( z ) − q ( z ) log q ( z ) ∇ λ log q ( z ) d z E z ∼ q ( z ) [( log p ( x , z ) − log q ( z )) ∇ λ log q ( z )]
即有
∇ λ E L B O = E z ∼ q ( z ) [ ( log p ( x , z ) − log q ( z ) ) ∇ λ log q ( z ) ] (3) \nabla_{\lambda}ELBO=E_{z\sim q(z)}[ (\log p(x,z)-\log q(z))\nabla_{\lambda} \log q(z) ]\tag3
∇ λ E L BO = E z ∼ q ( z ) [( log p ( x , z ) − log q ( z )) ∇ λ log q ( z )] ( 3 )
使用样本统计的话,z i z_i z i q ( z ) q(z) q ( z )
∇ λ E L B O = 1 N ∑ i = 1 N [ ( log p ( x , z i ) − log q ( z i ) ) ∇ λ log q ( z i ) ] \nabla_{\lambda}ELBO=\frac{1}{N}\sum_{i=1}^{N}[ (\log p(x,z_i)-\log q(z_i))\nabla_{\lambda} \log q(z_i) ]
∇ λ E L BO = N 1 i = 1 ∑ N [( log p ( x , z i ) − log q ( z i )) ∇ λ log q ( z i )]
EM 算法(Expectation-Maximum)传统贝叶斯推断
考虑离散情况下,我们需要求某个分布p p p θ \theta θ
θ ∗ = arg max θ ∑ i N log p ( x i ; θ ) \theta^*=\arg\max_{\theta} \sum_i^N\log p(x_i;\theta)
θ ∗ = arg θ max i ∑ N log p ( x i ; θ )
l ( θ ) = ∑ i log p ( x i ; θ ) = ∑ i log ∑ z i p ( x i , z i ; θ ) = ∑ i log ∑ z i Q i ( z i ) p ( x i , z i ; θ ) Q i ( z i ) ≥ ∑ i ∑ z i Q i ( z i ) log p ( x i , z i ; θ ) Q i ( z i ) \begin{aligned}
l(\theta)=\sum_i\log p(x_i;\theta)& =\sum_i\log\sum_{z_i}p(x_i,z_i;\theta) \\
&=\sum_i\log\sum_{z_i}Q_i(z_i)\frac{p(x_i,z_i;\theta)}{Q_i(z_i)} \\
&\geq\sum_i\sum_{z_i}Q_i(z_i)\log\frac{p(x_i,z_i;\theta)}{Q_i(z_i)}
\end{aligned}
l ( θ ) = i ∑ log p ( x i ; θ ) = i ∑ log z i ∑ p ( x i , z i ; θ ) = i ∑ log z i ∑ Q i ( z i ) Q i ( z i ) p ( x i , z i ; θ ) ≥ i ∑ z i ∑ Q i ( z i ) log Q i ( z i ) p ( x i , z i ; θ )
而似然函数可以写为:
log p ( x ) = D K L ( q ( z ) ∣ ∣ p ( z ∣ x ) ) + E q ( z ) [ log p ( x , z ) q ( z ) ] \log p(x)=D_{KL}({q(z)||p(z|x)})+E_{q(z)}[\log\frac{p(x,z)}{q(z)}]
log p ( x ) = D K L ( q ( z ) ∣∣ p ( z ∣ x ) ) + E q ( z ) [ log q ( z ) p ( x , z ) ]
EM算法输入:p ( x i ∣ z i ; θ ) , p ( z i ; θ ) , p ( z i ∣ x i ; θ ) p(x_i\mid z_i;\theta),p(z_i;\theta),p(z_i\mid x_i;\theta) p ( x i ∣ z i ; θ ) , p ( z i ; θ ) , p ( z i ∣ x i ; θ ) θ \theta θ X = { x i } i = 1 N X=\{x_i\}_{i=1}^{N} X = { x i } i = 1 N
问题:求解θ \theta θ
Random initialization θ \theta θ
(E-step) For each i , set Q i ( z i ) = p ( z i ∣ x i ; θ ) (M-step) Set θ = arg max θ ∑ i ∑ z i Q i ( z i ) log p ( x i , z i ; θ ) Q i ( z i ) = arg max θ ∑ i ∑ z i Q i ( z i ) log p ( x i , z i ; θ ) \begin{align*}
&\text{(E-step) For each } i, \text{ set } Q_i(z_i) = p(z_i \mid x_i; \theta) \\
&\text{(M-step) Set } \theta = \arg\max_{\theta} \sum_i \sum_{z_i} Q_i(z_i) \log \frac{p(x_i, z_i; \theta)}{Q_i(z_i)}=\arg\max_{\theta} \sum_i \sum_{z_i} Q_i(z_i) \log {p(x_i, z_i; \theta)}
\end{align*}
(E-step) For each i , set Q i ( z i ) = p ( z i ∣ x i ; θ ) (M-step) Set θ = arg θ max i ∑ z i ∑ Q i ( z i ) log Q i ( z i ) p ( x i , z i ; θ ) = arg θ max i ∑ z i ∑ Q i ( z i ) log p ( x i , z i ; θ )
E步骤用真实后验分布 for a choice of θ \theta θ
p ( z i ∣ x i ; θ ) = p ( x i ∣ z i ; θ ) p ( z i ; θ ) ∑ i p ( x i ∣ z i ; θ ) p ( z i ; θ ) p(z_i \mid x_i; \theta) = \frac{p(x_i \mid z_i; \theta) p(z_i; \theta)}{\sum _i p(x_i\mid z_i; \theta)p(z_i;\theta)}
p ( z i ∣ x i ; θ ) = ∑ i p ( x i ∣ z i ; θ ) p ( z i ; θ ) p ( x i ∣ z i ; θ ) p ( z i ; θ )
E步后,l ( θ ) l(\theta) l ( θ )
M步骤计算最优θ \theta θ Q i Q_i Q i Q i Q_i Q i θ \theta θ
EM算法同时优化θ \theta θ ,自然可以回答Problem scenario 中的三个问题,但是该算法在后验推断中的分母项存在很难的问题。
VAE这篇文章的motivation 是:
Intractability: the case where the integral of the marginal likelihood p θ ( x ) = ∫ p θ ( z ) p θ ( x ∣ z ) d z p_\theta(x) = \int p_\theta(z) p_\theta(x|z) dz p θ ( x ) = ∫ p θ ( z ) p θ ( x ∣ z ) d z p θ ( z ∣ x ) = p θ ( x ∣ z ) p θ ( z ) p θ ( x ) p_\theta(z|x) = \frac{p_\theta(x|z)p_\theta(z)}{p_\theta(x)} p θ ( z ∣ x ) = p θ ( x ) p θ ( x ∣ z ) p θ ( z ) EM algorithm cannot be used ), and where the required integrals for any reasonable mean-field VB algorithm are also intractable. These intractabilities are quite common and appear in cases of moderately complicated likelihood functions p θ ( x ∣ z ) p_\theta(x|z) p θ ( x ∣ z )
batch optimization is too costly
overall
p θ ( z ) p_{\theta}(z) p θ ( z ) θ \theta θ
p θ ( x ∣ z ) p_{\theta}(x|z) p θ ( x ∣ z )
q ϕ ( z ∣ x ) q_{\phi}(z|x) q ϕ ( z ∣ x ) p θ ( z ∣ x ) p_{\theta}(z|x) p θ ( z ∣ x )
3 task:
使用ML or MAP 求解 θ \theta θ
p θ ( z ∣ x ) p_{\theta}(z|x) p θ ( z ∣ x ) θ \theta θ marginal likelihood p θ ( x ) p_{\theta}(x) p θ ( x )
A method for learning the recognition model parameters ϕ \phi ϕ θ \theta θ
Objective function
The marginal likelihood is composed of a sum over the marginal likelihoods of individual datapoints log p θ ( x ( 1 ) , ⋯ , x ( N ) ) = ∑ i = 1 N log p θ ( x ( i ) ) \log p_{\theta}\left(x^{(1)},\cdots, x^{(N)}\right)=\sum_{i=1}^{N}\log p_{\theta}\left(x^{(i)}\right) log p θ ( x ( 1 ) , ⋯ , x ( N ) ) = ∑ i = 1 N log p θ ( x ( i ) )
log p θ ( x ( i ) ) = D K L ( q ϕ ( z ∣ x ( i ) ) ∣ ∣ p θ ( z ∣ x ( i ) ) ) + L ( θ , ϕ ; x ( i ) ) (4) \log p_{\theta}\left(x^{(i)}\right)=D_{KL}\left(q_{\phi}\left(z\mid x^{(i)}\right)\mid\mid p_{\theta}\left(z\mid x^{(i)}\right)\right)+\mathcal{L}\left(\theta,\phi; x^{(i)}\right)\tag{4}
log p θ ( x ( i ) ) = D K L ( q ϕ ( z ∣ x ( i ) ) ∣∣ p θ ( z ∣ x ( i ) ) ) + L ( θ , ϕ ; x ( i ) ) ( 4 )
The first RHS term is the KL divergence of the approximate from the true posterior. Since the KL-divergence is non-negative, the second RHS term L ( θ , ϕ ; x ( i ) ) \mathcal{L}\left(\theta,\phi; x^{(i)}\right) L ( θ , ϕ ; x ( i ) ) i i i
log p θ ( x ( i ) ) ≥ L ( θ , ϕ ; x ( i ) ) = E q ϕ ( z ∣ x ( i ) ) [ − log q ϕ ( z ∣ x ( i ) ) + log p θ ( x ( i ) , z ) ] \log p_{\theta}\left(x^{(i)}\right)\geq\mathcal{L}\left(\theta,\phi;x^{(i)}\right)=E_{q_{\phi}(z\mid x^{(i)})}\left[-\log q_{\phi}(z\mid x^{(i)})+\log p_{\theta}(x^{(i)},z)\right]
log p θ ( x ( i ) ) ≥ L ( θ , ϕ ; x ( i ) ) = E q ϕ ( z ∣ x ( i ) ) [ − log q ϕ ( z ∣ x ( i ) ) + log p θ ( x ( i ) , z ) ]
which can also be written as:
L ( θ , ϕ ; x ( i ) ) = − D K L ( q ϕ ( z ∣ x ( i ) ) ∣ ∣ p θ ( z ) ) + E q ϕ ( z ∣ x ( i ) ) [ log p θ ( x ( i ) ∣ z ) ] (5) \mathcal{L}\left(\theta,\phi; x^{(i)}\right)=-D_{KL}\left(q_{\phi}\left(z\mid x^{(i)}\right)\mid\mid p_{\theta}(z)\right)+E_{q_{\phi}\left(z\mid x^{(i)}\right)}\left[\log p_{\theta}\left(x^{(i)}\mid z\right)\right] \tag{5}
L ( θ , ϕ ; x ( i ) ) = − D K L ( q ϕ ( z ∣ x ( i ) ) ∣∣ p θ ( z ) ) + E q ϕ ( z ∣ x ( i ) ) [ log p θ ( x ( i ) ∣ z ) ] ( 5 )
最大化L \mathcal{L} L D K L D_{KL} D K L log p θ ( x ( i ) ) \log p_{\theta}(x^{(i)}) log p θ ( x ( i ) )
( θ ∗ , ϕ ∗ ) = arg max ∑ i ∈ [ N ] L ( θ , ϕ , x ( i ) ) (\theta^*,\phi^*)=\arg \max \sum_{i\in [N]}\mathcal{L}(\theta,\phi,x^{(i)})
( θ ∗ , ϕ ∗ ) = arg max i ∈ [ N ] ∑ L ( θ , ϕ , x ( i ) )
关于(5)的理解,第一部分KL divergence 是一个正则项,使得z z z
例如:若取p θ ( x ∣ z ) = 1 ( 2 π ) n σ θ e − ∣ ∣ x − μ θ ∣ ∣ 2 2 p_{\theta}(x|z)=\frac{1}{(\sqrt{2\pi})^n \sigma_{\theta}} e^{-\frac{||x-\mu_{\theta}||^2}{2}} p θ ( x ∣ z ) = ( 2 π ) n σ θ 1 e − 2 ∣∣ x − μ θ ∣ ∣ 2 μ θ = E x ∼ p θ ∗ ( x ∣ Z = z ) [ x ] , σ θ 2 = V a r x ∼ p θ ∗ ( x ∣ Z = z ) [ x ] \mu_{\theta}=\mathbb{E}_{x\sim p_{\theta^*}(x|Z=z)}[x],\sigma_{\theta}^2=\mathbb{Var}_{x\sim p_{\theta^*}(x|Z=z)}[x] μ θ = E x ∼ p θ ∗ ( x ∣ Z = z ) [ x ] , σ θ 2 = V a r x ∼ p θ ∗ ( x ∣ Z = z ) [ x ]
则第二部分变为E q ϕ ( z ∣ x ( i ) ) [ log ( ( 2 π ) n σ θ ) 2 ∣ ∣ x ( i ) − μ θ ∣ ∣ 2 ] E_{q_{\phi}(z|x^{(i)})}[\frac{\log \left( (\sqrt{2\pi})^n\sigma_{\theta} \right)}{2}||x^{(i)}-\mu_{\theta}||^2] E q ϕ ( z ∣ x ( i ) ) [ 2 l o g ( ( 2 π ) n σ θ ) ∣∣ x ( i ) − μ θ ∣ ∣ 2 ]
E q ϕ ( z ∣ x ( i ) ) [ log p θ ( x ( i ) ∣ z ) ] = E q ϕ ( z ∣ x ( i ) ) [ log ( ( 2 π ) n σ θ ) 2 ∣ ∣ x ( i ) − μ θ ∣ ∣ 2 ] = ∑ l ∈ [ L ] log ( ( 2 π ) n σ θ l ) 2 ∣ ∣ x ( i ) − μ θ l ∣ ∣ 2 μ θ l = x ^ l , σ θ l fixed for ∀ l = ∑ l ∈ [ L ] C ∣ ∣ x ( i ) − x ^ l ∣ ∣ 2 \begin{aligned}
E_{q_{\phi}\left(z\mid x^{(i)}\right)}\left[\log p_{\theta}\left(x^{(i)}\mid z\right)\right]=&E_{q_{\phi}(z|x^{(i)})}[\frac{\log \left( (\sqrt{2\pi})^n\sigma_{\theta} \right)}{2}||x^{(i)}-\mu_{\theta}||^2]\\
=&\sum_{l\in [L]}\frac{\log \left( (\sqrt{2\pi})^n\sigma_{\theta}^{l} \right)}{2}||x^{(i)}-\mu_{\theta}^{l}||^2\\
&\mu_\theta^{l}=\hat{x}^{l},\sigma_{\theta}^l \text{ fixed for } \forall l\\
=&\sum_{l\in [L]}C||x^{(i)}-\hat{x}^l||^2
\end{aligned}
E q ϕ ( z ∣ x ( i ) ) [ log p θ ( x ( i ) ∣ z ) ] = = = E q ϕ ( z ∣ x ( i ) ) [ 2 log ( ( 2 π ) n σ θ ) ∣∣ x ( i ) − μ θ ∣ ∣ 2 ] l ∈ [ L ] ∑ 2 log ( ( 2 π ) n σ θ l ) ∣∣ x ( i ) − μ θ l ∣ ∣ 2 μ θ l = x ^ l , σ θ l fixed for ∀ l l ∈ [ L ] ∑ C ∣∣ x ( i ) − x ^ l ∣ ∣ 2
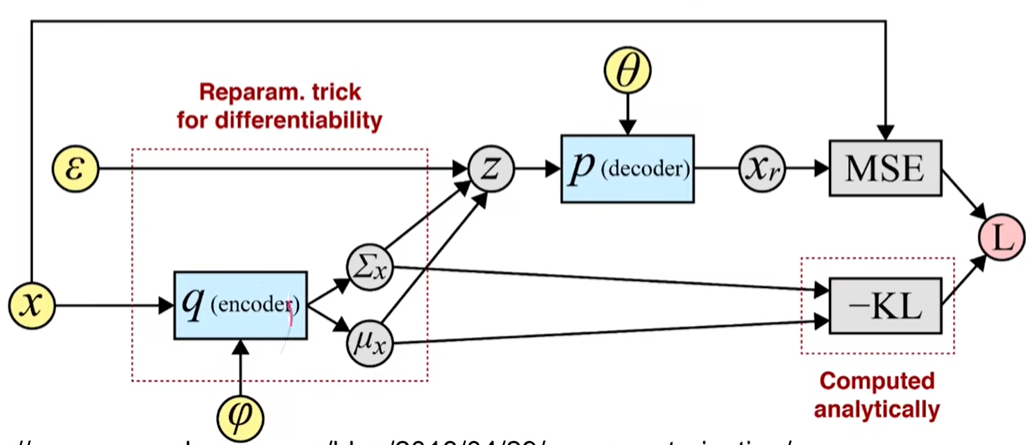
The SGVB estimator
我们需要对∇ θ , ϕ L ( θ , ϕ ; x ( i ) ) \nabla_{\theta,\phi}\mathcal{L}(\theta,\phi;x^{(i)}) ∇ θ , ϕ L ( θ , ϕ ; x ( i ) ) ∇ ϕ E q ϕ ( z ) [ f ( z ) ] = E q ϕ ( z ) [ f ( z ) ∇ q ϕ ( z ) log q ϕ ( z ) ] \nabla_{\phi} \mathbb{E}_{q_{\phi}(\mathbf{z})} \left[ f(\mathbf{z}) \right] = \mathbb{E}_{q_{\phi}(\mathbf{z})} \left[ f(\mathbf{z}) \nabla_{q_{\phi}(\mathbf{z})} \log q_{\phi}(\mathbf{z}) \right] ∇ ϕ E q ϕ ( z ) [ f ( z ) ] = E q ϕ ( z ) [ f ( z ) ∇ q ϕ ( z ) log q ϕ ( z ) ] f f f ϕ \phi ϕ
generic Stochastic Gradient Variational Bayes estimator
即重参数化的 Monte Carlo gradient estimator
q ϕ ( z ∣ x ) q_{\phi}(z|x) q ϕ ( z ∣ x )
for coding , probabilistic encoder 如何使用 gradient descent
是否可以给q ϕ ( z ∣ x ) q_{\phi}(z|x) q ϕ ( z ∣ x )
关于问题2,(5)式中KL divergence 告诉我们 q ϕ ( z ∣ x ) q_{\phi}(z|x) q ϕ ( z ∣ x ) p θ ( z ) p_{\theta}(z) p θ ( z ) p θ p_{\theta} p θ
for a chosen approximate posterior q ϕ ( z ∣ x ) q_{\phi}(z\mid x) q ϕ ( z ∣ x ) z ~ ∼ q ϕ ( z ∣ x ) \widetilde{z}\sim q_{\phi}(z\mid x) z ∼ q ϕ ( z ∣ x ) g ϕ ( ϵ , x ) g_{\phi}(\epsilon, x) g ϕ ( ϵ , x ) ϵ \epsilon ϵ
z ~ = g ϕ ( ϵ , x ) with ϵ ∼ p ( ϵ ) \widetilde{z}=g_{\phi}(\epsilon, x) \text{ with } \epsilon \sim p(\epsilon)
z = g ϕ ( ϵ , x ) with ϵ ∼ p ( ϵ )
We can now form Monte Carlo estimates of expectations of some function f ( z ) f(z) f ( z ) q ϕ ( z ∣ x ) q_{\phi}(z\mid x) q ϕ ( z ∣ x )
E q ϕ ( z ∣ x ( i ) ) [ f ( z ) ] = E p ( ϵ ) [ f ( g ϕ ( ϵ , x ( i ) ) ) ] ≃ 1 L ∑ l = 1 L f ( g ϕ ( ϵ ( l ) , x ( i ) ) ) where ϵ ( l ) ∼ p ( ϵ ) \mathbb{E}_{q_{\phi}(z\mid x^{(i)})}\left[f(z)\right] = \mathbb{E}_{p(\epsilon)}\left[f\left(g_{\phi}\left(\epsilon, x^{(i)}\right)\right)\right] \simeq \frac{1}{L}\sum_{l=1}^{L} f\left(g_{\phi}\left(\epsilon^{(l)}, x^{(i)}\right)\right) \text{ where } \epsilon^{(l)} \sim p(\epsilon)
E q ϕ ( z ∣ x ( i ) ) [ f ( z ) ] = E p ( ϵ ) [ f ( g ϕ ( ϵ , x ( i ) ) ) ] ≃ L 1 l = 1 ∑ L f ( g ϕ ( ϵ ( l ) , x ( i ) ) ) where ϵ ( l ) ∼ p ( ϵ )
We apply this technique to the variational lower bound , yielding our generic Stochastic Gradient Variational Bayes (SGVB) estimator L ~ A ( θ , ϕ ; x ( i ) ) ≃ L ( θ , ϕ ; x ( i ) ) \widetilde{\mathcal{L}}^{A}(\theta,\phi; x^{(i)}) \simeq \mathcal{L}(\theta,\phi; x^{(i)}) L A ( θ , ϕ ; x ( i ) ) ≃ L ( θ , ϕ ; x ( i ) )
L ~ A ( θ , ϕ ; x ( i ) ) = 1 L ∑ l = 1 L log p θ ( x ( i ) , z ( i , l ) ) − log q ϕ ( z ( i , l ) ∣ x ( i ) ) where z ( i , l ) = g ϕ ( ϵ ( i , l ) , x ( i ) ) and ϵ ( l ) ∼ p ( ϵ ) (6) \begin{align*}
\widetilde{\mathcal{L}}^{A}(\theta,\phi; x^{(i)}) &= \frac{1}{L}\sum_{l=1}^{L} \log p_{\theta}(x^{(i)}, z^{(i, l)}) - \log q_{\phi}(z^{(i, l)} \mid x^{(i)}) \\
\text{where} \quad z^{(i, l)} &= g_{\phi}(\epsilon^{(i, l)}, x^{(i)}) \quad \text{and} \quad \epsilon^{(l)} \sim p(\epsilon)
\end{align*} \tag{6}
L A ( θ , ϕ ; x ( i ) ) where z ( i , l ) = L 1 l = 1 ∑ L log p θ ( x ( i ) , z ( i , l ) ) − log q ϕ ( z ( i , l ) ∣ x ( i ) ) = g ϕ ( ϵ ( i , l ) , x ( i ) ) and ϵ ( l ) ∼ p ( ϵ ) ( 6 )
不考虑p θ p_{\theta} p θ x ( i ) , ϕ , ϵ ( l ) x^{(i)},\phi,\epsilon ^{(l)} x ( i ) , ϕ , ϵ ( l ) z ( i , l ) z^{(i,l)} z ( i , l )
可以选择q ϕ ( z ∣ x ) q_{\phi}(z|x) q ϕ ( z ∣ x ) g ϕ g_{\phi} g ϕ z z z ϵ \epsilon ϵ
second version of the SGVB estimator
KL-divergence D K L ( q ϕ ( z ∣ x ( i ) ) ∣ ∣ p θ ( z ) ) D_{KL}\left(q_{\phi}\left(z\mid x^{(i)}\right)\mid\mid p_{\theta}(z)\right) D K L ( q ϕ ( z ∣ x ( i ) ) ∣∣ p θ ( z ) )
因为p θ ( z ) p_{\theta}(z) p θ ( z ) q ϕ ( z ∣ x ) q_{\phi}(z|x) q ϕ ( z ∣ x ) p θ ( z ) = N ( z ; 0 , I ) p_{\theta}(z)=\mathcal{N}(z;\mathbf{0},\mathbf{I}) p θ ( z ) = N ( z ; 0 , I ) q ( z ∣ x ) = N ( z ; μ , σ 2 ) q(z|x)=\mathcal{N}(z;\mathbf{\mu},\mathbf{\sigma}^2) q ( z ∣ x ) = N ( z ; μ , σ 2 ) J J J z z z
− D K L ( ( q ϕ ( z ) ∥ p θ ( z ) ) ) = ∫ q θ ( z ) ( log p θ ( z ) − log q θ ( z ) ) d z = 1 2 ∑ j = 1 J ( 1 + log ( ( σ j ) 2 ) − ( μ j ) 2 − ( σ j ) 2 ) -D_{KL}((q_{\phi}(\mathbf{z}) \| p_{\theta}(\mathbf{z}))) = \int q_{\theta}(\mathbf{z}) \left( \log p_{\theta}(\mathbf{z}) - \log q_{\theta}(\mathbf{z}) \right) d\mathbf{z}
= \frac{1}{2} \sum_{j=1}^{J} \left( 1 + \log((\sigma_j)^2) - (\mu_j)^2 - (\sigma_j)^2 \right)
− D K L (( q ϕ ( z ) ∥ p θ ( z ))) = ∫ q θ ( z ) ( log p θ ( z ) − log q θ ( z ) ) d z = 2 1 j = 1 ∑ J ( 1 + log (( σ j ) 2 ) − ( μ j ) 2 − ( σ j ) 2 )
The above equation can be regarded as the regularization of ϕ \phi ϕ
Such that only the expected reconstruction error E q ϕ ( z ∣ x ( i ) ) [ log p θ ( x ( i ) ∣ z ) ] \mathbb{E}_{q_{\phi}\left(z\mid x^{(i)}\right)}\left[\log p_{\theta}\left(x^{(i)}\mid z\right)\right] E q ϕ ( z ∣ x ( i ) ) [ log p θ ( x ( i ) ∣ z ) ]
This yields a second version of the SGVB estimator L ~ B ( θ , ϕ ; x ( i ) ) ≃ L ( θ , ϕ ; x ( i ) ) \widetilde{\mathcal{L}}^{B}\left(\theta,\phi; x^{(i)}\right)\simeq\mathcal{L}\left(\theta,\phi; x^{(i)}\right) L B ( θ , ϕ ; x ( i ) ) ≃ L ( θ , ϕ ; x ( i ) )
L ~ B ( θ , ϕ ; x ( i ) ) = − D K L ( q ϕ ( z ∣ x ( i ) ) ∣ ∣ p θ ( z ) ) + 1 L ∑ l = 1 L ( log p θ ( x ( i ) ∣ z ( i , l ) ) ) where z ( i , l ) = g ϕ ( ϵ ( i , l ) , x ( i ) ) and ϵ ( l ) ∼ p ( ϵ ) (7) \begin{array}{l}
\widetilde{\mathcal{L}}^{B}\left(\theta,\phi; x^{(i)}\right)=-D_{KL}\left(q_{\phi}\left(z\mid x^{(i)}\right)\mid\mid p_{\theta}(z)\right)+\frac{1}{L}\sum_{l=1}^{L}\left(\log p_{\theta}\left(x^{(i)}\mid z^{(i, l)}\right)\right)\\
\text{where}\quad z^{(i, l)}=g_{\phi}\left(\epsilon^{(i, l)}, x^{(i)}\right)\text{ and}\epsilon^{(l)}\sim p(\epsilon)
\end{array}\tag{7}
L B ( θ , ϕ ; x ( i ) ) = − D K L ( q ϕ ( z ∣ x ( i ) ) ∣∣ p θ ( z ) ) + L 1 ∑ l = 1 L ( log p θ ( x ( i ) ∣ z ( i , l ) ) ) where z ( i , l ) = g ϕ ( ϵ ( i , l ) , x ( i ) ) and ϵ ( l ) ∼ p ( ϵ ) ( 7 )
Given multiple datapoints from a dataset X X X N N N
L ( θ , ϕ ; X ) ≃ L ~ M ( θ , ϕ ; X M ) = N M ∑ i = 1 M L ~ ( θ , ϕ ; x ( i ) ) (8) \mathcal{L}(\theta,\phi; X)\simeq\widetilde{\mathcal{L}}^{M}\left(\theta,\phi; X^{M}\right)=\frac{N}{M}\sum_{i=1}^{M}\widetilde{\mathcal{L}}\left(\theta,\phi; x^{(i)}\right)\tag{8}
L ( θ , ϕ ; X ) ≃ L M ( θ , ϕ ; X M ) = M N i = 1 ∑ M L ( θ , ϕ ; x ( i ) ) ( 8 )
where the minibatch X M = { x ( i ) } i = 1 M X^{M}=\left\{x^{(i)}\right\}_{i=1}^{M} X M = { x ( i ) } i = 1 M M M M X X X N N N
AEVB algorithm
Algorithm 1 Minibatch version of the Auto-Encoding VB (AEVB) algorithm. Either of the two SGVB estimators can be used. We use settings M = 100 M=100 M = 100 L = 1 L=1 L = 1
θ , ϕ ← \theta, \phi \leftarrow θ , ϕ ← repeat
X M ← X^{M} \leftarrow X M ← M M M ϵ ← \epsilon \leftarrow ϵ ← p ( ϵ ) p(\epsilon) p ( ϵ ) g ← ∇ θ , ϕ L ~ M ( θ , ϕ ; X M , ϵ ) g \leftarrow \nabla_{\theta,\phi}\widetilde{\mathcal{L}}^{M}(\theta,\phi; X^{M},\epsilon) g ← ∇ θ , ϕ L M ( θ , ϕ ; X M , ϵ ) (8) )θ , ϕ ← \theta, \phi \leftarrow θ , ϕ ← g g g
until convergence of parameters ( θ , ϕ ) (\theta, \phi) ( θ , ϕ ) return θ , ϕ \theta, \phi θ , ϕ
review 3 tasks
使用ML or MAP 求解 θ \theta θ
p θ ( z ∣ x ) p_{\theta}(z|x) p θ ( z ∣ x ) θ \theta θ marginal likelihood p θ ( x ) p_{\theta}(x) p θ ( x )
encoder q ϕ ( z ∣ x ) q_{\phi}(z|x) q ϕ ( z ∣ x )
关于task 1
求解ML问题,极大似然参数估计: (4) 式中 左边 就是 ML的对数似然函数,所以最大化(variational) lower bound 就是求解ML问题;
求解MAP问题,贝叶斯参数估计(后验参数估计):MAP对数似然函数为∑ i = 1 N log p θ ( x ( i ) ) + log δ ( θ ) \sum_{i=1}^{N}\log p_{\theta}(x^{(i)})+\log \delta(\theta) ∑ i = 1 N log p θ ( x ( i ) ) + log δ ( θ ) δ ( θ ) \delta(\theta) δ ( θ ) θ \theta θ
关于 task 3,paper附录中 使用了 类MCMC技巧求得的隐变量后验分布+求AEVB求得的p θ ( x ( i ) ∣ z l ) p_{\theta}(x^{(i)}|z^{l}) p θ ( x ( i ) ∣ z l ) p θ ( x ( i ) ) p_{\theta}(x^{(i)}) p θ ( x ( i ) )